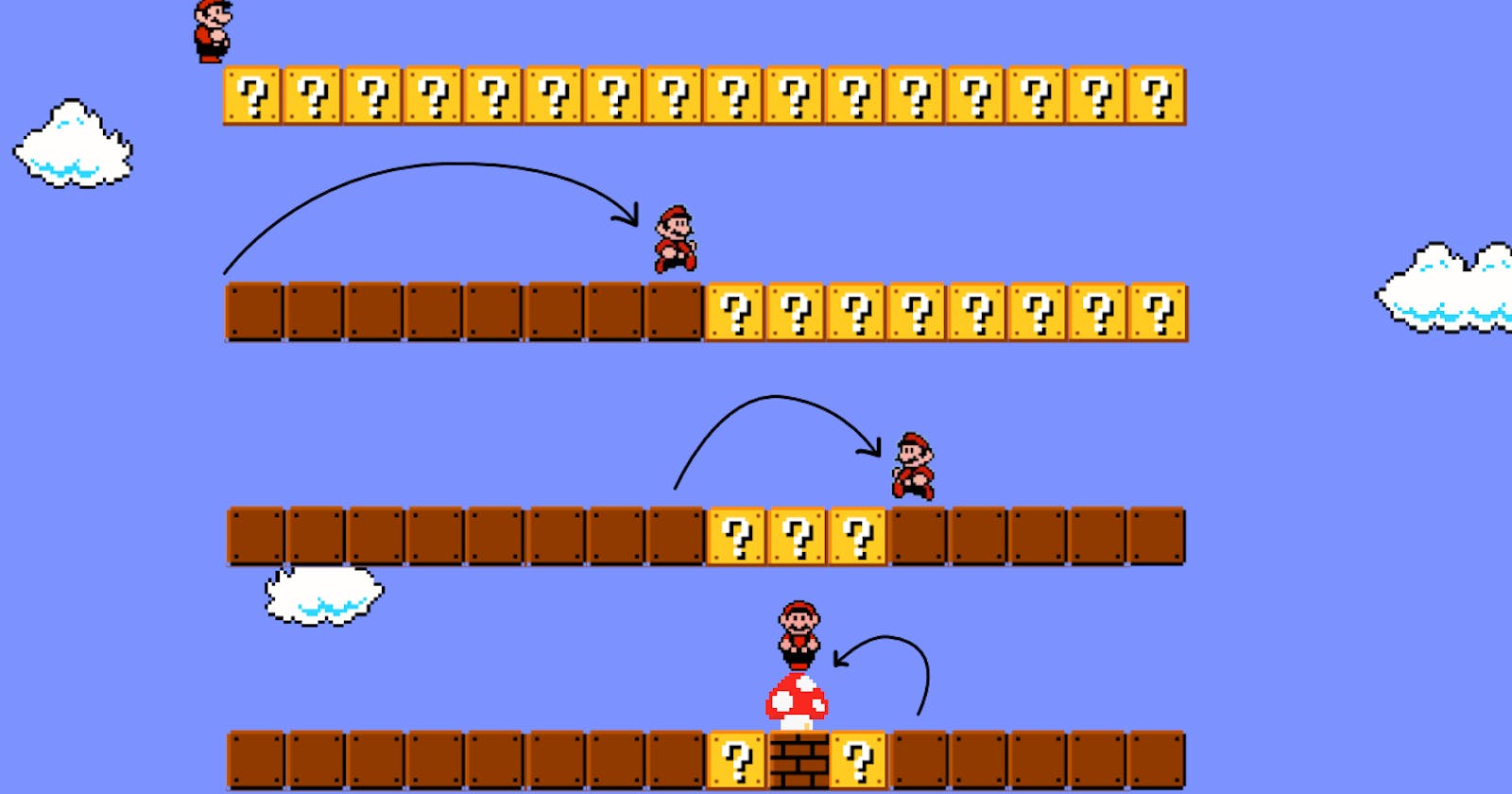
Binary search (BS) is one of the most important concepts in CP algorithms in general. You will use binary search everywhere.

We will see what is BS, the different implementations of BS, what are the things to remember while implementing BS, what is search space in BS, and a lot more.

So first,

What is binary search?

If you have ever opened a dictionary or even a book with an index. You always know whether to look ahead or turn back to previous pages depending on the page number you are currently on.

E.g. If you are looking for page number 100 and are currently on 76 you surely know you have to go ahead. Or if you are looking for the word Search in the dictionary and your current page’s first word is xylophone you are sure that the word surely lies somewhere in previous pages (as long as it is lexicographically aligned).

To be honest, the idea of Binary search is a lot more than that. But for our current discussion, it is okay to avoid further anomalies. The problem we currently going to discuss is using binary search to find elements in sorted arrays(or any other container vector in c++, list in python).

Now here I would like to define sorted. Sorted could mean any particular order which is throughout the array. Whether it be a number in ascending or descending order, words aligned alphabetically, or any function whose graph is linear.

So first how do you implement BS, here we are looking at the problem of finding whether an element x exists in the sorted array arr . We can check if the element at the current index (arr[idx]) is the same as x if it is, then we have found the element. If not then let’s compare the elements at the current index. If x is more than the current element x (arr[idx] < x), then we surely know the element (if exists) is at the right side of the index.

Now, the only question that remains is how we decide where to start and how to keep changing the current index.

For this, we take two variables l and r. initialize l with 0 (l = 0) and r with size of the array – 1 (r = size_of_arr - 1). We are just taking the first and last index of the array (0-based indexing).

Note: There are different implementations where we fix them, r = size_of_arrwe will talk about that later.

And then we have another variable (mid) which is just the average of l and r (rounded off to a lower integer)

mid = (l + r) / 2

Now depending upon the value at arr[idx] we will keep on changing the value of l and r .

Demo Code:

bool search(int arr[], int size, int x) {
    int l = 0, r = size - 1;
    while(l <= r) {
        int mid = (l + r) / 2;
        if(arr[mid] == x) {
            return true;
        }
        if(arr[mid] < x) {
            l = mid + 1;
        } else {
            r = mid - 1;
        }
    }
    return false;
}

If you have got the idea then try this problem (for c++ users: use 4byte int and array instead of vector to avoid getting TLE)

The basic idea of binary search is simple. But implementations could be tricky and not always accurate. The very first bug in this code was seen in java programming language. READ HERE

Every variable comes with certain limits like int in c++ can only be of size 4 byes (2 for older compilers).

So the maximum value of a four-byte integer could only be 2147483647 and the minimum is -2147483648 (Note: the first bit of this is used as a sign bit henve -2^31 to +2^31 - 1) READ HERE

So what's the issue?

Now assume that at some point at binary search you get l = 2147483647 and r = 2147483647 so What will be the sum of those two? 4294967294 which is way more than an int in c++. This causes an overflow error. In C++ any value which is greater than 2147483647 (2^31 - 1) gets started back with (-2^31).

So the value of mid at this point would be something like

#include<iostream>
using namespace std;

int main() {
    int l = 2147483647;
    int r = 2147483647;
    int temp = l + r;
    cout << temp << endl;
    int mid = (l + r) / 2;
    cout << mid << endl;
}

//Output
// -2
// -1

If you are not sure why -1 and -2 please understand overflow errors in c++. (if you do 2147483647 + 1 it becomes - 2147483648).

So, how to overcome this issue?

Well, you can use another way to calculate the mid, which is just another way of writing the same thing with basic arithmetic changes.

mid = l + (r - l) / 2

If you expand you can see it is the same as the mid above. You will see this implementation a lot of times. If you want to see if you can get rid of this overflow I recommend you solve LEETCODE PROBLEM.

This might be a good time to tell you, readers, Binary search isn't just about searching through arrays but reducing the current search space to half with each iteration.

So what do I mean by search space?

In the above example when we started with l = 0 and r = n - 1 (n is the size of the array). So the search space in this step is everything from the first to last index i.e all the array then we check the mid element with x (element to be found) And we assign l = mid or r = mid depending on the values of arr[mid] and x . So at each step, we get rid of half the space to search and worry about.

Now let's look at another usage of binary usage. Now you know if you have an element and you want to check if it exists, you can use binary search. But what if you have an element and you just need to check if an element greater than or equal to this element exist?

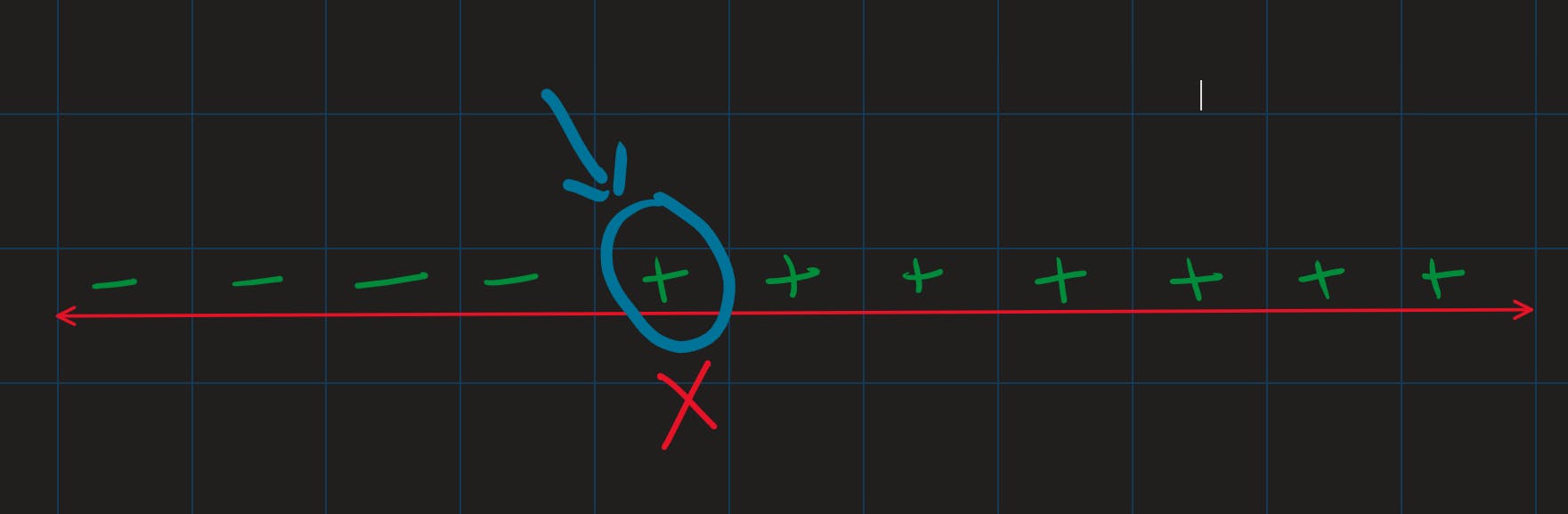
See the above diagram, all the - in this indicates an element lesser than x and all the + indicates all the elements greater than x. So we need to find the position marked in blue. How can we do that? Yes! Using Binary Search.

Let's look at how we used binary search in the previous example. We would do all the things exactly as same as we did above but this time just for simplification we will assume r to be equal to n (instead of n - 1). I will explain 'why?' in a bit.

But all the other things will be the same. We will check if arr[mid] is greater than x or less than x or equal to x in all these cases we have to change our search space (or simply values of l and r). Let's assume we have an array as {1, 3, 6, 10, 16, 21, 29}

And we have element 15, And we want to know at what index in this sorted array values start to appear to be greater than 15.

Let's do the same thing, assign l = 0 and r = n (Note: n and not n - 1).

This time let's take a closer look at each step

{1, 3, 6, 10, 16, 21, 29}

Value: 1 3 6 10 16 21 29

Index: 0 1 2 3 4 5 6

x = 15

l = 0 and r = 7

mid = l + r2

mid = 3

arr[mid] = 10

arr[mid] < x

So, assign

l = mid

l = 3

mid = 3 + 72

mid = 5

arr[mid] = 21

arr[mid] > x

so, assign

r = mid

r = 5

l = 3, r = 5

mid = 3 + 52

mid = 4

Now we have arr[mid] = 16

And as 16 is less than 15, we should assign r = mid.

And we should continue ahead till l <= r. But remember where we initialized our l = 0 and r = n

So at some point l = r then we might reach mid = n, As you know the size of the array is n, and when we do zero-based indexing we must end at (n - 1), So why have I decided to start the r at n?

Well, the answer is simple! I just talked about search space. I want my l to represent my final answer and r to represent the value next to it (in other words, index that can never be the answer Hence the ‘n’).

That's why in this case we define the stop condition to be l < r and not l <= r.

Another way to write would be r - l > 1

But we still have one more question left

What if arr[mid] = x?

At that time what should we do?

Well, as we are trying to find the start index we must go to the right side of the mid, but if we go to the right side then we are assigning r = mid and what if this is the only place where we have x and not before that?

Then we just lost our answer!!

One thing we could do is we can create a separate variable and every time we get a value greater value store it, and return the smallest integer. Works fine but let's just stick to l and r patterns for now :)

So, we use a different approach where we initialise l with 0 and r with n (as discussed earlier).

And check if arr[mid] < x, and if it is we surely know the answer lies ahead of mid so we can just assign l = mid + 1

else in every other case, we do r = mid

Now, Wait!

why?

I hope this part is pretty clean why are we assigning r = mid when arr[mid] > x, but what if arr[mid] == x?

That is the condition,

Let's assume, at some point

int arr[] = {1, 2, 4, 10, 11, 11, 12, 13, 14};

int x = 11

so we initialize l = 0 and r = 9

We calculate mid, and everything is normal

So later step when

l = 0, r = 4

mid = (l + r) / 2

mid = 2

As obviously arr[mid] = 4 < x

So we assing l = mid + 1

l = 3

Now l = 3 and r = 4

so mid become (l + r) / 2 which is 3

Now when you check again arr[mid] which is still less than x, so assign l = mid + 1

That's when it takes the place of r and we get out of the loop.

So, our answer is currently stored at l

The implementation:

#include<iostream>
using namespace std;

int lower_bound(int arr[], int n, int x) {
    int l = 0, r = n;
    while (l < r) {
        int mid =  l + (r - l) / 2;
        if (x <= arr[mid]) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    return l;
}

int main() {
    int n = 9;
    int arr[] = {1, 2, 4, 10, 11, 11, 12, 13, 14};
    cout << "When value of x is 11: " << lower_bound(arr, n, 11) << endl;
    cout << "When value of x is 15: " << lower_bound(arr, n, 15) << endl;

    return 0;
}

/*
Output:
When value of x is 11: 4
When value of x is 15: 9
*/

You might have seen the lower_bound function in c++. This works the same as discussed above. You can use this function as shown below:

#include<iostream>
#include<algorithm>
using namespace std;

int main() {
    const int N = 7;
    int arr[N] = {1, 3, 6, 10, 16, 21, 29};
    int x = 15, y = 16, z = 17;
    /*
        You can use vector too, just use appropriate iterators.
    */
    int idxForX = lower_bound(arr, arr + N, x) - arr;
    int idxForY = lower_bound(arr, arr + N, y) - arr;
    int idxForZ = lower_bound(arr, arr + N, z) - arr;

    cout << "X: " << idxForX << endl;
    cout << "Y: " << idxForY << endl;
    cout << "Z: " << idxForZ << endl;

    return 0;
}

/*
Output:
X: 4
Y: 4
Z: 5
*/

If you give value x as an input to the lower_bound function then you would get the lowest index within the range [x, INT_MAX).

If you give value x as an input to upper_bound then you would get the lowest index within range (x, INT_MAX).

Note: [ means value included in the range ( means value excluded from the range.

Happy Reading!

TeckBakers/iRatherFear

Any query and suggestion are always welcome - Aman Nadaf