Technique

It is a simple technique that can give you an end array after performing range queries of the form update(l, r, x).

NOTE: update(l, r, x) means add x to all the elements in an array within the range l to r. arr[l] += x, arr[l + 1] += x, arr[l + 2] += x, ... arr[r] += x.

The difference array work on a simple technique that when you add something to a range in an array the difference between two elements remains the same except for the boundary of the range.

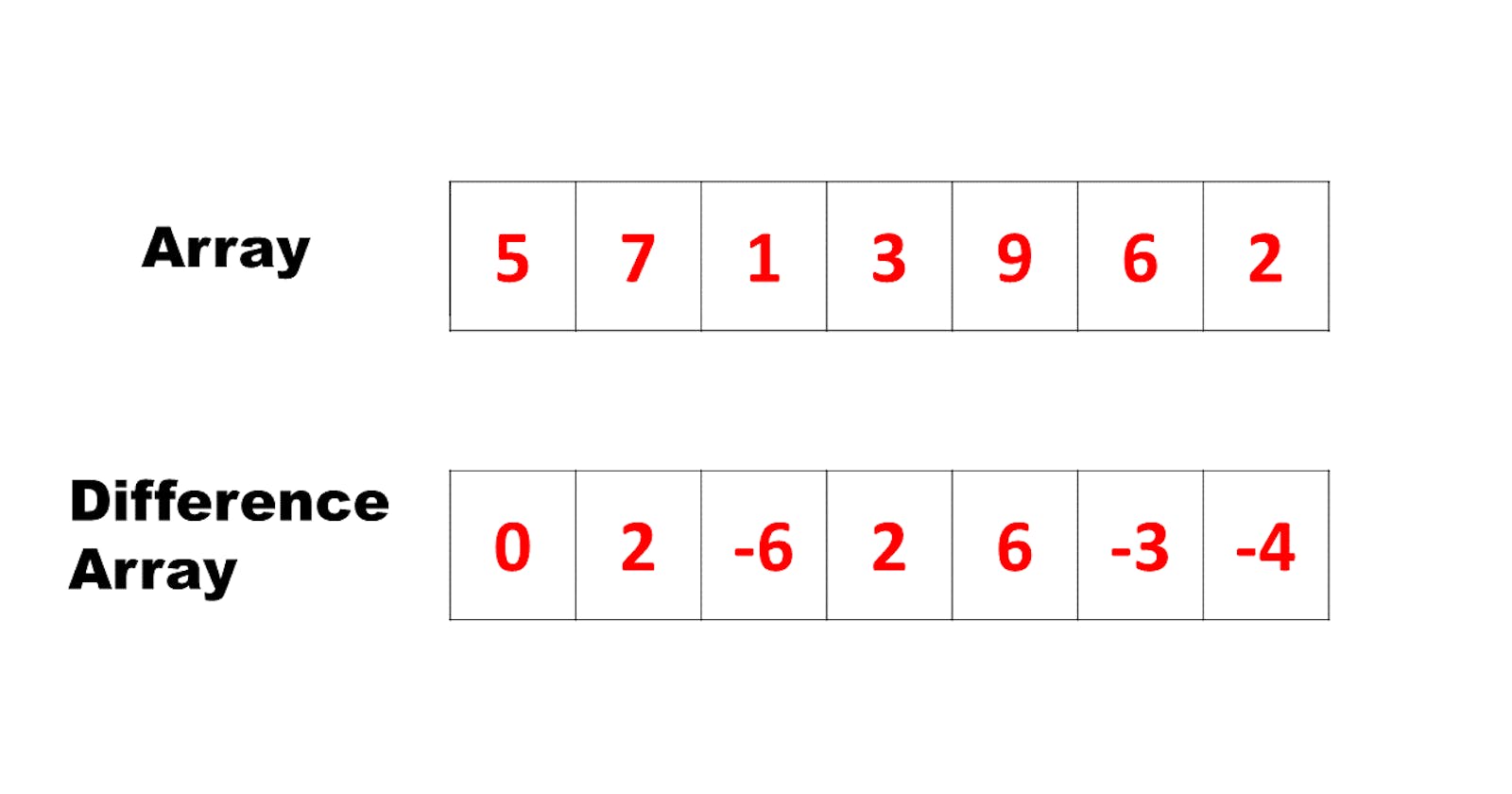
E.g. The arr is an array of size 5. diffArr stores all the differences between the two elements.

$$Where, \space \space diffArr[i] = arr[i] - arr[i - 1] \space \space 1 \le i < N$$

$$\begin{align} & arr[5] = { a_1, a_2, a_3, a_4, a_5 } \ & diffArr[5] = { 0, a_2 - a_1, a_3 - a_2, a_4 - a_3, a_5 - a_4 } \end{align}$$

Now when you add X to all elements from index 2 to 4 you get

$$\begin{align} & arr[5] = { a_1, a_2 + x, a_3 + x, a_4 + x, a_5 } \ & diffArr[5] { 0, (a_2 + x) - a_1, (a_3 + x) - (a_2 + x), (a_4 + x) - (a_3 + x), a_5 - (a_4 + x) } \ & diffArr[5] = { 0, a_2 + x - a_1, a_3 - a_2, a_4 - a_3, a_5 - a_4 - x } \end{align}$$

As you can see, everything remained the same except the 2nd and 5th elements. 2nd element increases by X and 5th element decreases by X.

Now if we add Y to the 3rd and 4th elements.

$$arr[5] = { a_1, a_2 + x, a_3 + x + y, a_4 + x + y, a_5 }$$

The difference array becomes:

$$\begin{align} & diffArr[6] = { 0, a_1, (a_3 + x + y) - (a_2 + x), (a_4 + x + y) - (a_3 + x + y), a_5 - (a_4 + x + y)} \ & diffArr[6] = { 0, a_2 - a_1 + x, a_3 - a_2 + y, a_4 - a_3, a_5 - a_4 - x - y } \end{align}$$

Again, the only values that changed are 3rd and 5th.

Now, we can use this property to do some range query operations.

NOTE: This is not how you generally implement difference arrays. I will explain that in a bit.

In the start, we can initiate a difference array as described above,

When we update the range (l, r), only lth and r + 1th element changes by x.

So, we will increment diffArr[l] by x and decrement diffArr[r + 1] by x.

int N = 7; //size of array
vector<int> arr{5, 7, 1, 3, 9, 6, 2};
vector<int> diffArr(N + 1, 0);

void initiateDiffArray() {
    for(int i = 1; i < N; i++) {
        diffArr[i] = arr[i] - arr[i - 1];    
    }
}
void update(int l, int r, int val) {
    diffArr[l] += val;
    diffArr[r + 1] -= val;
}

Now, as you can see all the changes to the first element are pretty apparent. They can easily be checked by adding diffArr[0] to the arr[0].

And, if we have our first element and we know the definition of diffArr[i].We can easily get all elements of an array using:

In, the first case

And we can calculate the rest of the array using the same technique.

class DiffArray
{
private:
int arrSize;
vector<int> arr;
vector<int> diffArr;
public:
    DiffArray(vector<int> v) {
        arr = v;
        arrSize = (int) arr.size();
        diffArr = vector<int> (arrSize + 1, 0);
        for(int i = 1; i < arrSize; i++) {
            diffArr[i] = arr[i] - arr[i - 1];
        }
    }

    void update(int l, int r, int x) {
        diffArr[l] += x;
        diffArr[r + 1] -= x;
    }

    vector<int> getArray() {
        arr[0] = arr[0] + diffArr[0];
        for(int i = 1; i < arrSize; i++) {
            arr[i] = diffArr[i] + arr[i - 1];
        }
        return arr;
    }
};

In the above code, you can see that you are adding arr[i - 1] to arr[i], then you will add arr[i] to arr[i + 1]. Which means you are taking the pre-sum. So, you can do this in the Difference array at first then add that to the actual array.

vector<int> getArray() {    
    for(int i = 1; i < arrSize; i++) {
        diffArr[i] = diffArr[i] + diffArr[i - 1];    
    }        
    for(int i = 0; i < arrSize; i++) {
        arr[i] += diffArr[i];
    }
    return arr;
}

The above implementation is more general.

---

Problem: Karen and Coffee.

In this problem, you are given N number of suggested range of temperatures. If some temperature is suggested by at least K times, it is called admissible.

After that, you are given Q queries. Each query is of the form a and b. In each query, you are required to find the number of admissible temperatures within the range a and b(inclusive).

For, the first part we can directly use the Difference Array. Where indices of array will work as temperatures and values stored in it will be incremented as we get the suggestions from recipes.

And then we will use the prefix sum on the above array. And after pre_sum[b] - pre_sum[a - 1] we will get the value of admissible integer temperatures within the range a and b.

NOTE: In this, we will not start our difference array with vector(array) but with the maximum temperature(integer). Because in the initial array, all the integers will be 0.

Here, is the implementation:

#include<bits/stdc++.h>
using namespace std;

const int MAX_TEMP = 200001;

class DiffArray
{
private:
int arrSize;
vector<int> arr;
vector<int> diffArr;
public:
    DiffArray(int n) {
        arrSize = n;
        arr = vector<int> (arrSize, 0);
        diffArr = vector<int> (arrSize + 1, 0);
        for(int i = 1; i < arrSize; i++) {
            diffArr[i] = arr[i] - arr[i - 1];
        }
    }

    void update(int l, int r, int x) {
        diffArr[l] += x;
        diffArr[r + 1] -= x;
    }

    vector<int> getArray() {
        arr[0] = arr[0] + diffArr[0];
        for(int i = 1; i < arrSize; i++) {
            arr[i] = diffArr[i] + arr[i - 1];
        }
        return arr;
    }
};

int main() {
    int n, k, q;
    cin >> n >> k >> q;

    DiffArray obj(MAX_TEMP);

    for(int i = 0; i < n; i++) {
        int l, r;
        cin >> l >> r;
        obj.update(l, r, 1);    
    }
    vector<int> diffArr = obj.getArray();

    //we will use the same array as pre_sum array
    for(int i = 0; i < MAX_TEMP; i++) {
        if(diffArr[i] >= k) {
            diffArr[i] = 1;
        } else {
            diffArr[i] = 0;
        }
        if(i) {
            diffArr[i] += diffArr[i - 1];
        }
    }

    for(int i = 0; i < q; i++) {
        int a, b;
        cin >> a >> b;
        cout << diffArr[b] - diffArr[a - 1] << endl;
    }
    return 0;
}

Template for Difference array:

class DiffArray
{
private:
int arrSize;
vector<int> arr;
vector<int> diffArr;
public:
    DiffArray(vector<int> v) {
        arr = v;
        arrSize = (int) arr.size();
        diffArr = vector<int> (arrSize + 1, 0);
        for(int i = 1; i < arrSize; i++) {
            diffArr[i] = arr[i] - arr[i - 1];
        }
    }

    DiffArray(int n) {
        arrSize = n;    
        arr = vector<int> (arrSize, 0);
        diffArr = vector<int> (arrSize + 1, 0);
    }

    void update(int l, int r, int x) {
        diffArr[l] += x;
        diffArr[r + 1] -= x;
    }

    vector<int> getArray() {
        if(arrSize < 1) {
            return arr;    
        }
        arr[0] = arr[0] + diffArr[0];
        for(int i = 1; i < arrSize; i++) {
            arr[i] = diffArr[i] + arr[i - 1];
        }
        return arr;
    }
};

Thank You for reading!

If you have any queries, Do not forget to contact us below: