Hello Readers,

Introduction

Here, I will be discussing an interesting data structure called "Fenwick Tree". Its structure was proposed by Boris Ryabko and was described by Peter Fenwick in an article from 1994. It is also called the "Binary Indexed Tree(BIT)".

Its job is similar to a segment tree. But the code is very short and easy to write. Here, we will be discussing the classical Dynamic Range Sum Queries problem. Where you are given an array and you have to constantly update some index of the array and simultaneously solve online queries on that array.

Concept

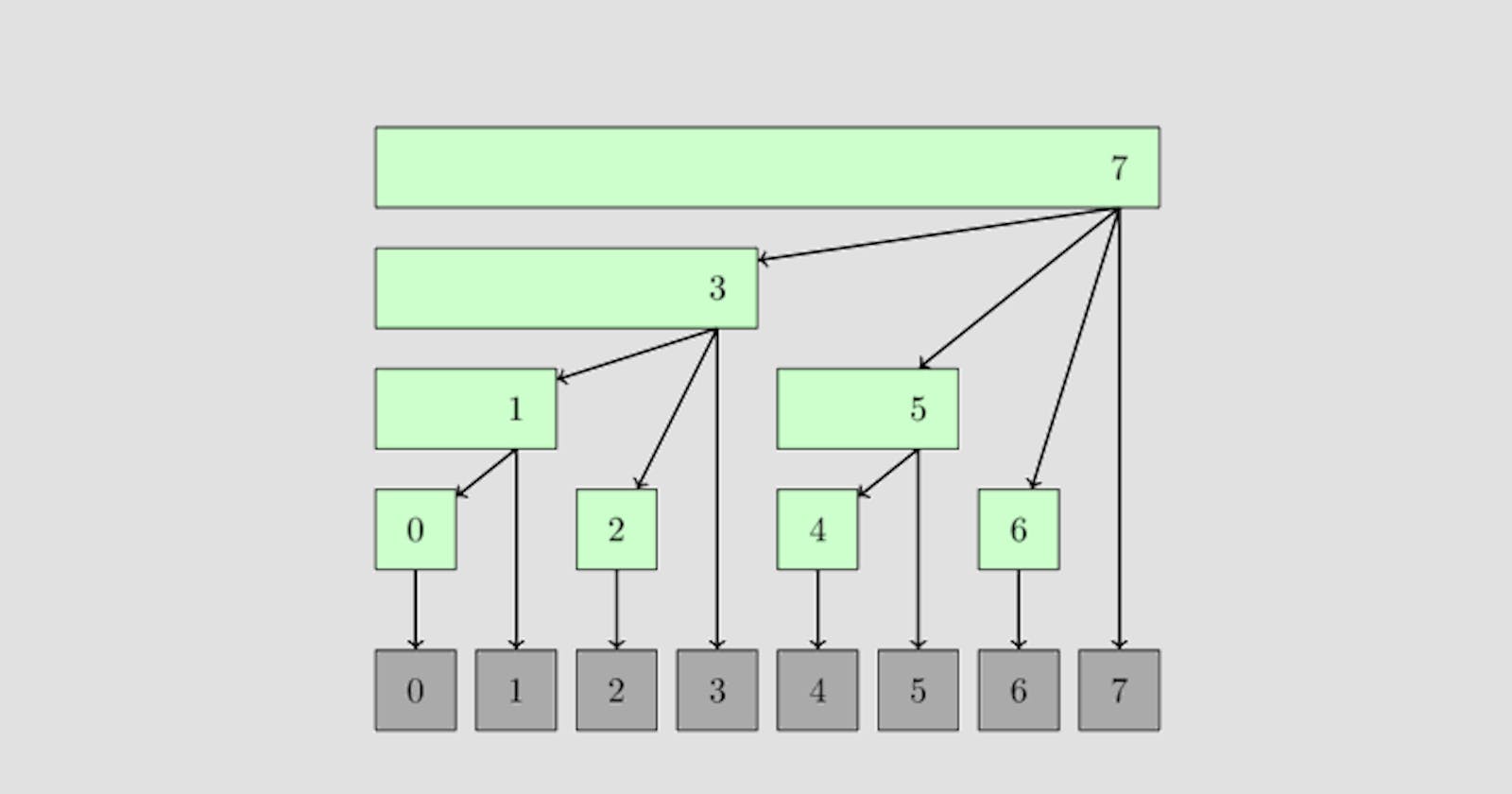
While considering Fenwick Tree you will assume our initial array to have 1-based indexing. An array with n elements will have the Fenwick Tree of n + 1 nodes (because we are using 1-based indexing).

NOTE: ( denoting excluding par(i) and ] denoting including i. More Ways

The tree will have 0 at the root position denoting an empty sum(0).

At level 1 you will have all the indices with the form

$$2^i$$

At level 2

$$2^i + 2^{i - k}, \space 0 \le i - k$$

Basically, at each level, you will have indices with the same number of bits as the level number. E.g. In the first level, you will have only those indices with a number of bits equal to 1.

Each element at the index i in Fenwick Tree will have summation stored from (par(i), i]. For each node i, its parent is the node you get after subtracting LSB(i).

NOTE: LSB(x) indicates the least significant bit of x. It can be calculated as shown below

$$LSB(x) = (x \& (-x))$$

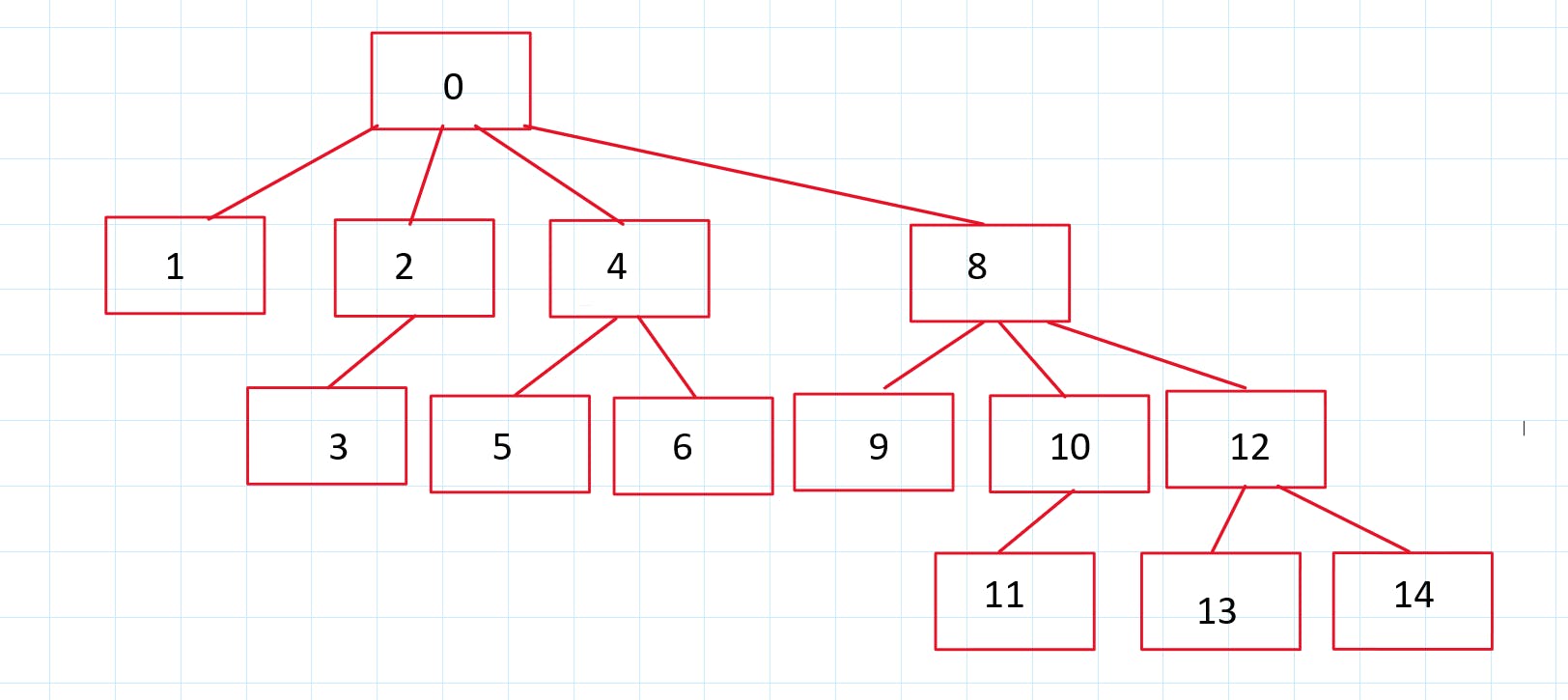
So, let's create a simple Fenwick Tree for an array with size 14.

First, let's create a 0th index it has an empty sum(0).

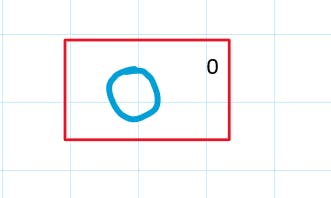
At the first level, we will have all the powers of 2 which are less than or equal to N(15).

$$2^0, 2^1, 2^2, 2^3 \le N$$

i.e 1, 2, 4, 8.

They all will have a value of zero stored at first.

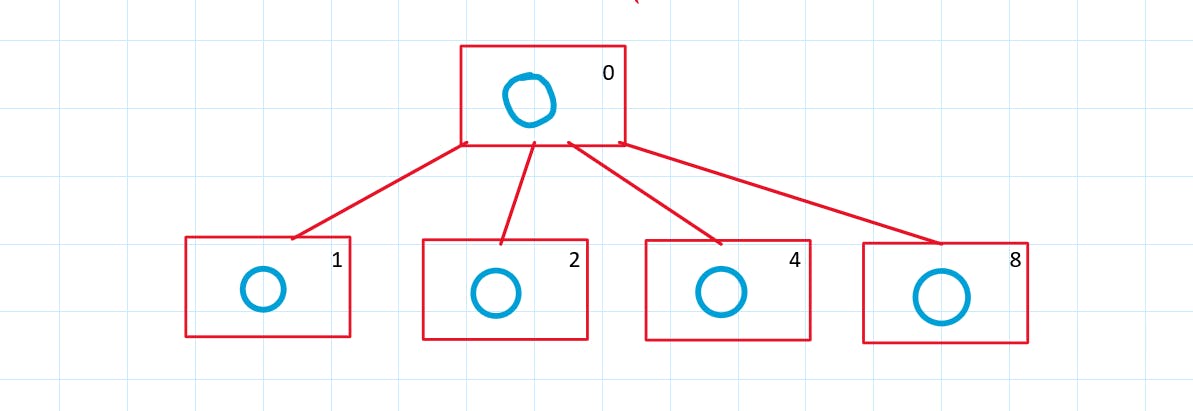
Now, for the next level let's look at the formula we saw before.

As, you can see for all the nodes (1, 2, 4, 8), if you subtract its LSB you will get zero.

Now, for the third level, you will have the following tree.

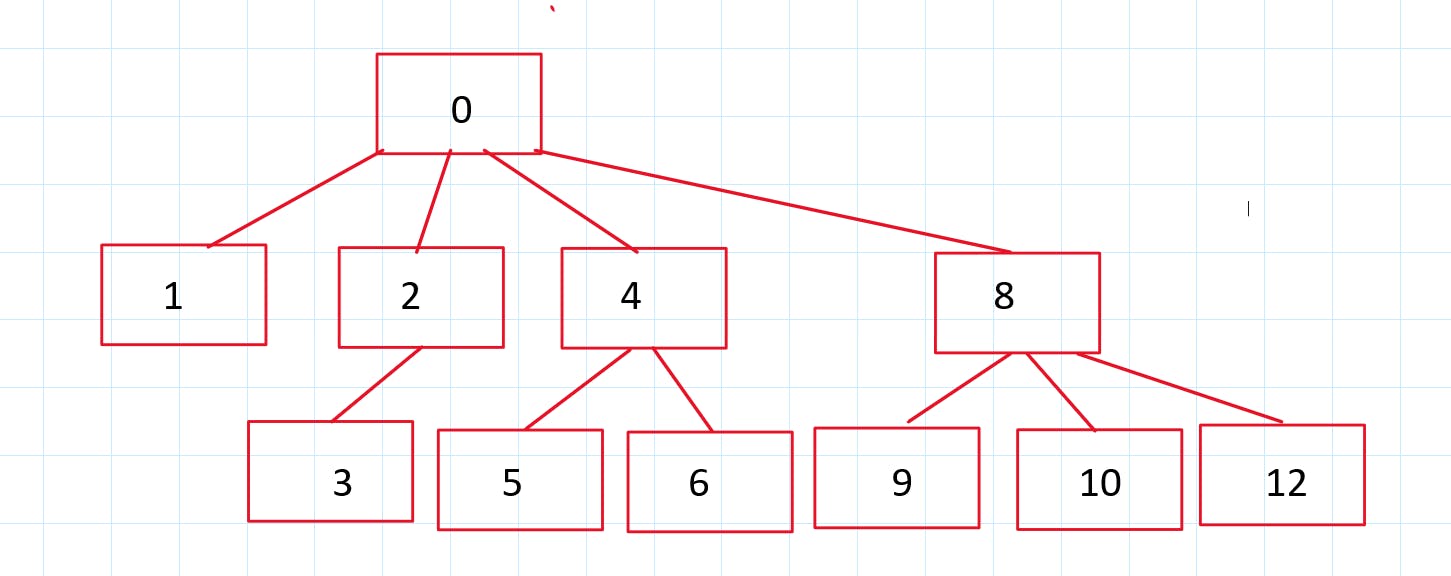
NOTE: I have only marked indexes in the above tree.

Now, finally, you have all the remaining nodes i.e 11, 13, 14

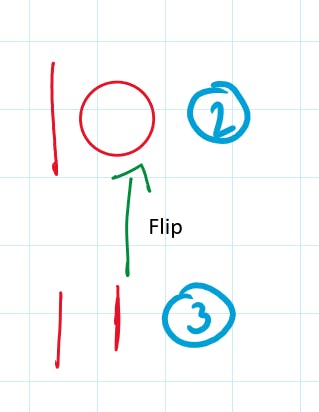
If you need a simpler way to derive children nodes you can one by one change all the zero bits to one till you reach the LSB.

For index 2, the binary representation is 10. If you one by one flip all zeroes you will get its children nodes' indices.

Similarly for 8,

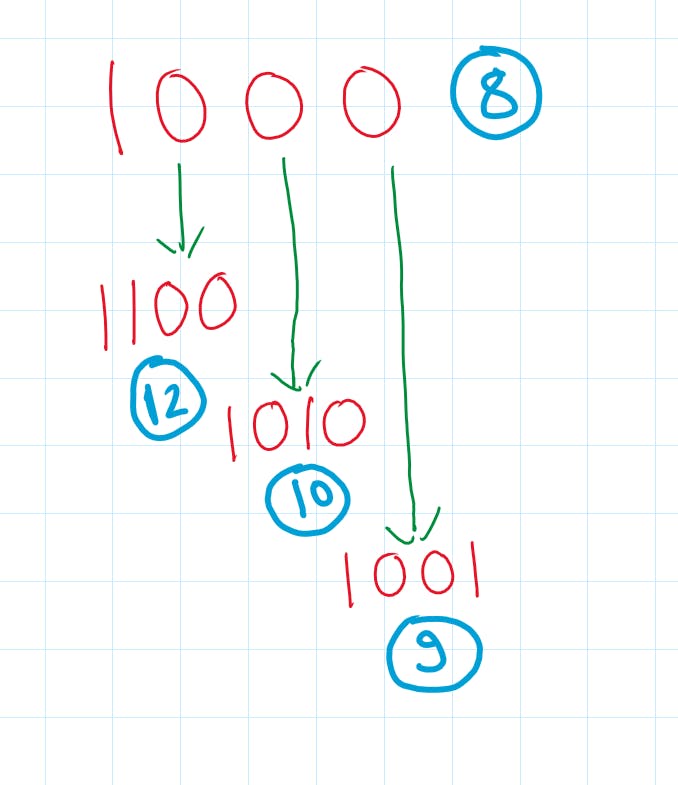
You can also see that as you are only flipping one zero to one you can always have 1 bit more in children nodes' indices than the parent.

Update

When you have to update any indices in the array you can just simply update the node and all its parent nodes.

To go from the children node to the parent node simply subtract the LSB from the children node to reach the parent node.

$$parent(i) = i - (i \& (-i))$$

Also remember that, if you are creating a Fenwick tree for an array, you need to update all the elements individually.

Fenwick Tree over Segment Tree

Fenwick Tree, also known as Binary Indexed Tree (BIT), is a tree data structure that is used to efficiently perform range queries and updates on an array of numbers. It is a data structure that is often used in competitive programming as well as in other areas such as computer science and engineering.

One of the main benefits of Fenwick Tree over Segment Tree is that it requires less memory. While Segment Tree stores information for all possible intervals, Fenwick Tree only stores information for some intervals, making it more space-efficient. We use 4 times the size of the array in the segment tree.

Another benefit of Fenwick Tree is its simplicity. It is relatively easy to implement compared to Segment Tree. The update and query operations are also faster and simpler than Segment Tree. Fenwick Tree is more suited for dynamic problems that require frequent updates to the array.

Finally, Fenwick Tree is a more specialized data structure for certain types of problems, such as prefix sum or cumulative frequency problems. In such problems, Fenwick Tree is significantly faster and simpler than Segment Tree.

Dynamic Range Sum Queries Solution

#include<iostream>
#include<vector>
#define int long long int
using namespace std;

class Fenwick
{
private:
    int arrSize;
    vector<int> BIT;
    int LBS(int idx) {
        return (idx & (-idx));
    }
public:
    Fenwick(int num) {
        arrSize = num + 1;
        BIT = vector<int> (arrSize);
    }
    Fenwick(vector<int> v) {
        arrSize = (int) v.size() + 1;
        BIT = vector<int> (arrSize);
        for(int i = 0; i < arrSize - 1; i++) {
            update(i + 1, v[i]);
        }
    }

    void update(int idx, int val) {
        while(idx < arrSize) {
            BIT[idx] += val;
            idx += LBS(idx);
        } 
    }

    int query(int idx) {
        int ans = 0;
        while(idx > 0) {
            ans += BIT[idx];
            idx -= LBS(idx);
        }
        return ans;
    }
};

int32_t main() {
    int n, q;
    cin >> n >> q;
    vector<int> v(n);
    for(int i = 0; i < n; i++) {
        cin >> v[i];
    }

    Fenwick obj(v);
    for(int i = 0; i < q; i++) {
        int type;
        cin >> type;
        if(type == 1) {
            int k, u;
            cin >> k >> u;
            obj.update(k, u - v[k - 1]); 
            /*  We are note adding u to v[k] 
                but change v[k] to u, which is 
                equivalent to adding u - v[k] to v[k]*/
            v[k - 1] = u;
        } else {
            int a, b;
            cin >> a >> b;
            cout << obj.query(b) - obj.query(a - 1) << endl;
        }
    }
    return 0;
}

Thank You for Reading, if you have any feedback to share do not forget to write a comment.

You can also contact us below,