Table of contents
Hello,
Sieve of Eratosthenes
I hope you all know what Seive is. This article will give you different variations of sieves.
So, for those who don't know what "Sieve of Eratosthenes" is, it is just a faster way to calculate all the prime numbers between 1 to n (in general, n can be upto 1e5/1e6). With time complexity O(n * log(log(n))) and space complexity O(n).
So, how do we do it?
Well, we just iterate i from 2 to n, and at each step we cancel out all the multiples of i. Here is a beautiful GIF from Wikipedia.
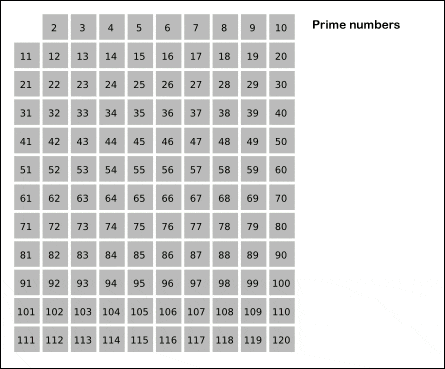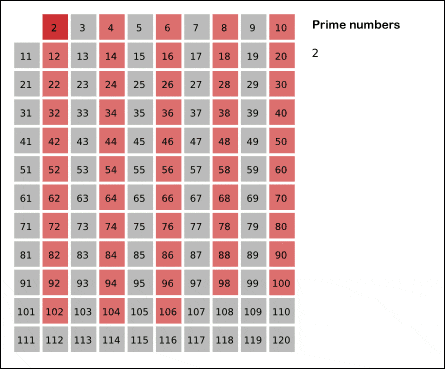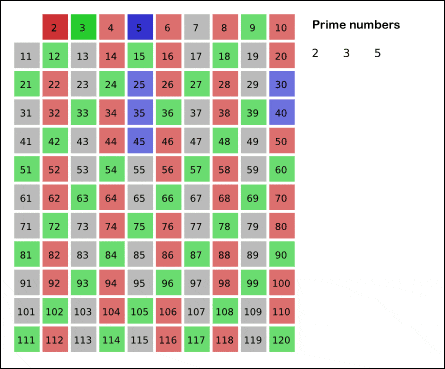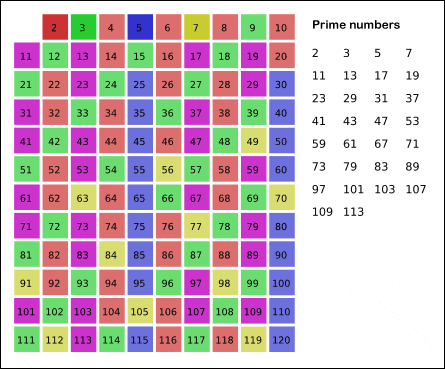
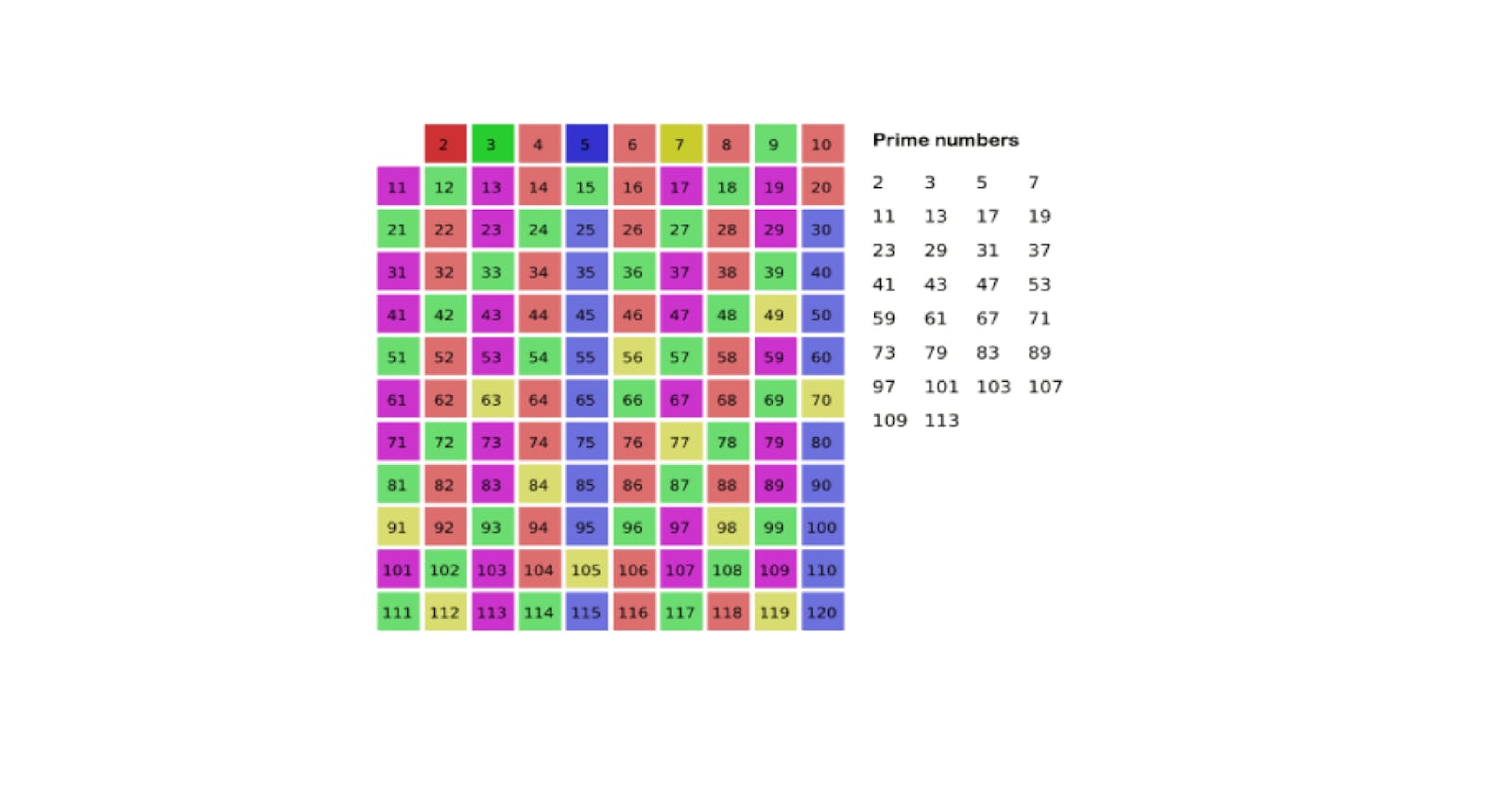
I will explain with a smaller example where N = 25.
So let's create 25 boxes.
For now, just ignore 1 as it is neither a prime number nor a composite.
s of 2.
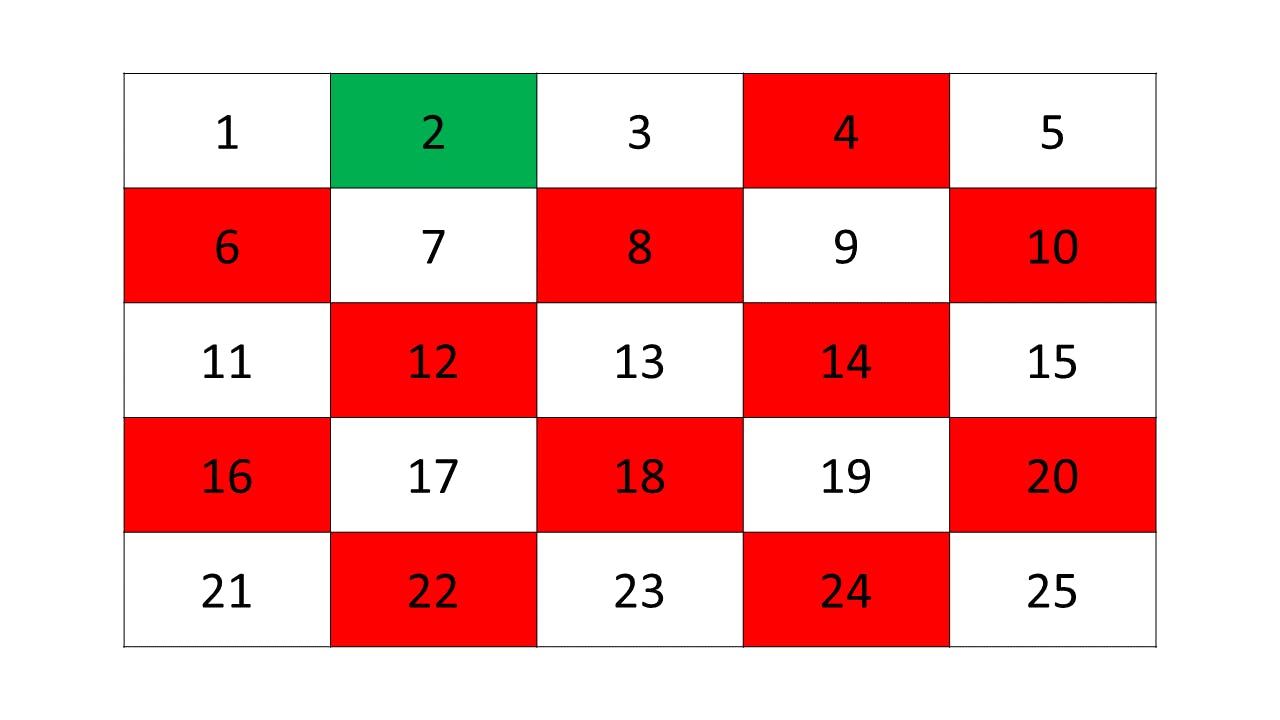
So, let's start from 2 and mark all the multiple.
Note: Green color indicates the prime number.
All, the numbers are marked red. As you can see all the numbers with 2 as a prime factor are marked.
Let's go ahead and do the same for 3
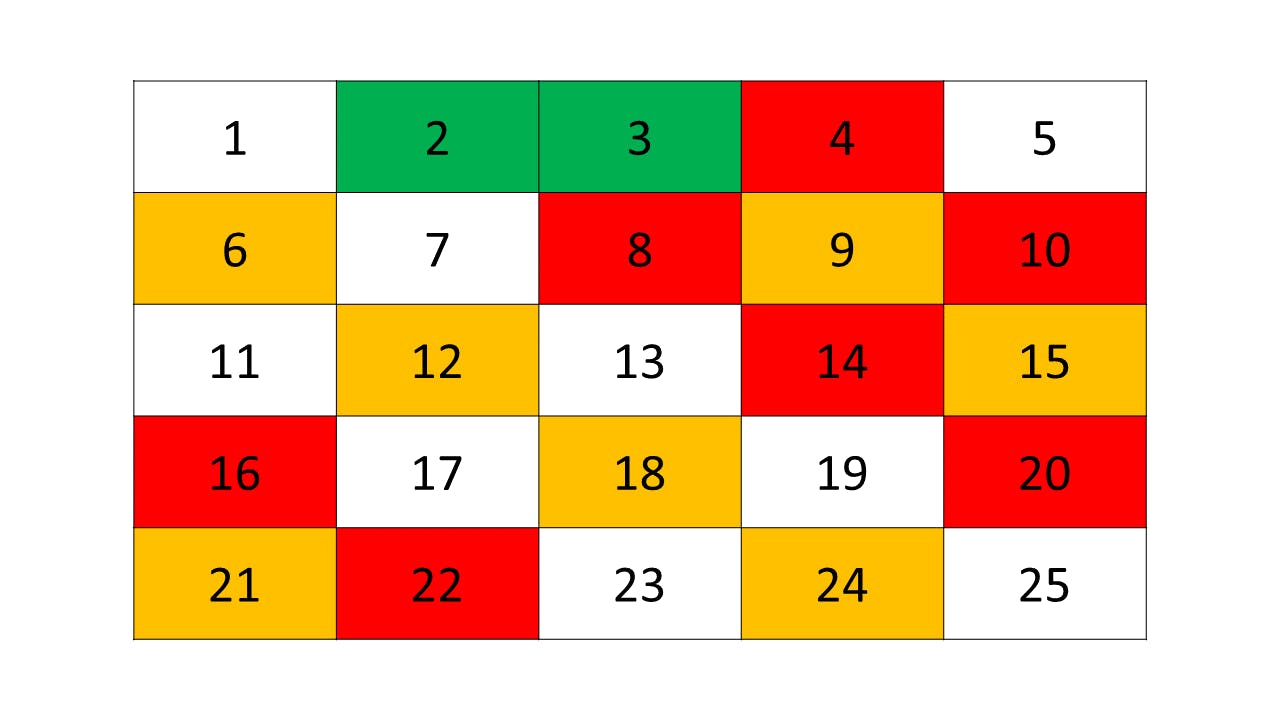
3 is marked green and all its multiple are marked amber.
For 5,
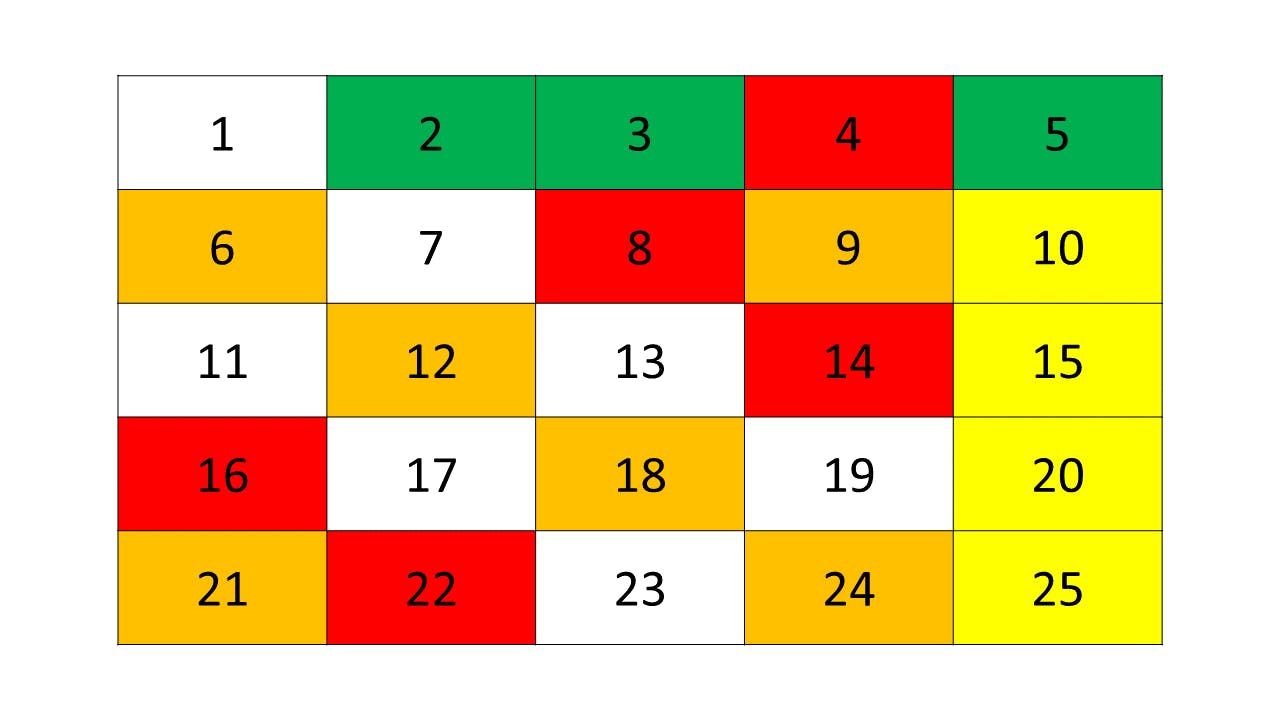
for 7,

for 11,

Now, for the rest, we will mark them as green as they don't have any multiples in the range of 1 to 25.
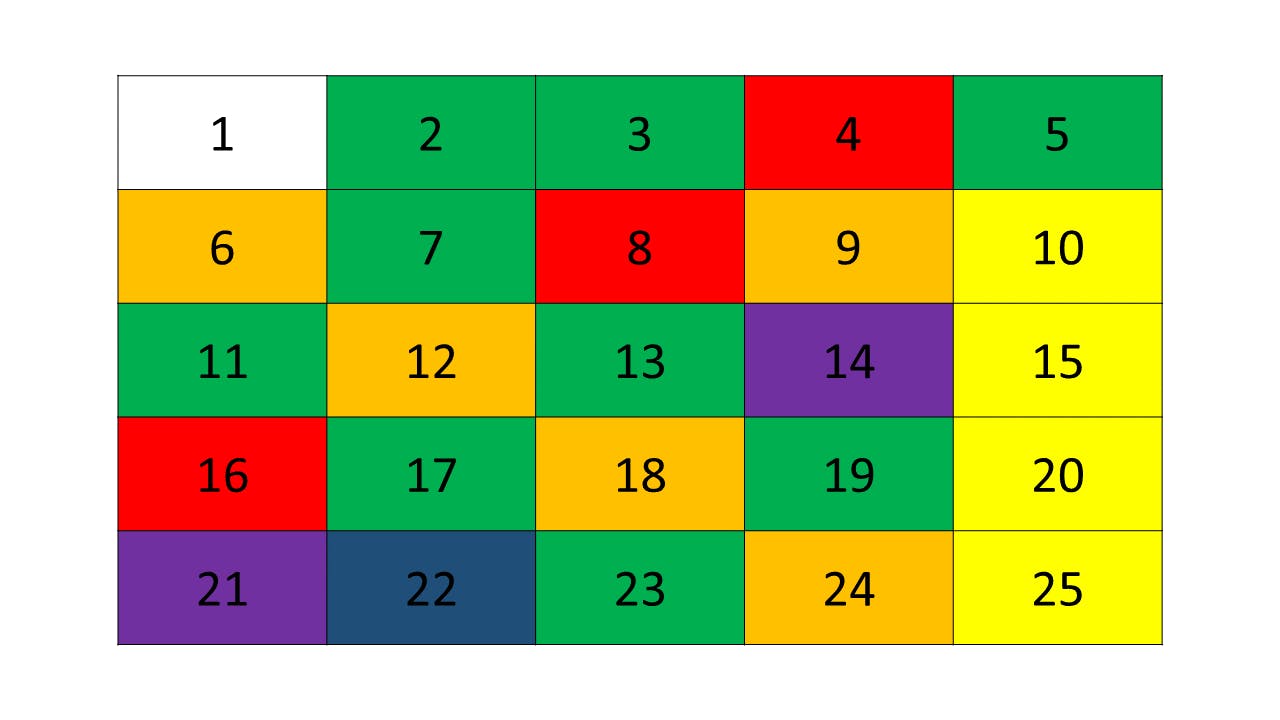
Now, you can see we start with 2, marking all the numbers whose prime factor is 2.
Similarly, we do the same thing for 3, 5, 7, 11, 13, and the rest.
We always mark elements if they have a factor, so we only remain with prime numbers. This way we can always ensure that only the prime numbers remain at the end.
vector<int> seive() {
const int N = 100001;
vector<int> hash(N, false);
vector<int> prime;
for(int i = 2; i < N; i++) {
if(hash[i] == false) {
prime.push_back(i);
int cur = i + i;
while(cur < N) {
hash[cur] = true;
cur += i;
}
}
}
return prime;
}
Now, we can optimize it further. As you can see when we start with 2, we mark all the even numbers. So, we no longer have to worry about even numbers. For that we can just take the even number out at the start.
vector<int> seive(int N) {
vector<int> prime;
if(N <= 1) {
return prime;
}
vector<int> hash(N, false);
for(int i = 4; i < N; i += 2) {
hash[i] = true;
}
prime.push_back(2);
for(int i = 3; i < N; i++) {
if(hash[i] == false) {
prime.push_back(i);
int cur = i + i;
while(cur < N) {
hash[cur] = true;
cur += i;
}
}
}
return prime;
}
Now, one more observation is that if we add two odd numbers, we always get an even number. We have already marked out the even numbers so we can ignore them for now.
E.g.
For i = 3
we continue to mark down 6, 9, 12, 16, ...
So instead we can mark alternatively.
vector<int> seive(int N) {
vector<int> prime;
if(N <= 1) {
return prime;
}
vector<int> hash(N, false);
for(int i = 4; i < N; i += 2) {
hash[i] = true;
}
prime.push_back(2);
for(int i = 3; i < N; i++) {
if(hash[i] == false) {
prime.push_back(i);
int cur = i; (we have to ignore the first one)
int sum = i + i;
while(cur + sum < N) {
hash[cur + sum] = true;
cur += sum;
}
}
}
return prime;
}
We also know that, if the number is not prime then it at least has one prime factor which is less than the square root of that number.
i.e. if n is the number we want to mark and it's not prime then it would have been marked by any number which is less than root n.
vector<int> seive(int N) {
vector<int> prime;
if(N <= 1) {
return prime;
}
vector<int> hash(N, false);
for(int i = 4; i < N; i += 2) {
hash[i] = true;
}
prime.push_back(2);
for(int i = 3; i < N; i++) {
if(hash[i] == false) {
prime.push_back(i);
int cur = i * i;
while(cur < N) {
hash[cur] = true;
cur += i;
}
}
}
return prime;
}
We, can use this way to efficiently find all the prime numbers form 1 to n.
Euler's Totient Function
$$\begin{align} & \text{Euler's Totient function is denoted by } \phi (n) \newline \end{align}$$
Euler's totient function denotes the number of positive integers which are coprime to n and which are also less than (or equal to) n.
$$\phi(1) = 1$$
There are some properties of Euler's totient function that we will use. (I will prove this in a future article).
$$\displaylines{ \phi(m \times n) = \phi(m) \times \phi(n) \newline \phi(p) = p - 1 \space (\text{p is a prime number}) \newline \phi(p^a) = p^a - p^{a - 1} \space \text{(p is a prime number)} }$$
Now, we know we can represent any number in the form
$$n = p_1^{a_1} \times p_2^{a_2} \times p_3^{a_3} \times .. p_i ^ {a_i}$$
So, using the above properties we can write,
$$\begin{align} & \phi(n) = \phi(p_1^{a_1} \times p_2^{a_2} \times p_3^{a_3} \times .. p_i ^ {a_i} ) \newline & \phi(n) = \phi(p_1^{a_1}) \times \phi(p_2^{a_2}) \times .. \phi(p_i^{a_i}) \newline & \phi(n) = (p_1^{a_1} - p_1^{a_1 - 1}) \times (p_2^{a_2} - p_2^{a_2 - 1}) \times .. (p_i^{a_i} - p_i^{a_i - 1}) \newline & \phi(n) = (p_1^{a_1} \times (1 - \frac{1}{p_1})) \times (p_2^{a_2} \times (1 - \frac{1}{p_2})) \times ... (p_i^{a_i} \times (1 - \frac{1}{p_i})) \newline & \phi(n) = (p_1^{a_1} \times p_2^{a_2} \times ... p_i ^ {a_i}) \times ((1 - \frac{1}{p_1}) \times (1 - \frac{1}{p_2}) \times .. (1 - \frac{1}{p_i})) \newline & \text{Now we know, } n = (p_1^{a_1} \times p_2^{a_2} \times ... p_i ^ {a_i}) \newline & \phi(n) = n \times (1 - \frac{1}{p_1}) \times (1 - \frac{1}{p_2}) \times .. (1 - \frac{1}{p_i}) \end{align}$$
Now, we can find Euler's totient for any value of n using the above formula.
We can again use "Sieve", Now, instead of marking the value as true or false. We will initialize the value of each box with its own index. At every iteration, we will decrement it by n / i.
vector<int> eulers_totient(int N) {
vector<int> phi(N + 1);
for(int i = 0; i <= N; i++) {
phi[i] = i;
}
for(int i = 2; i <= N; i++) {
if(phi[i] == i) {
phi[i] = i - 1; //for prime numbers
int cur = 2 * i;
while(cur <= N) {
phi[cur] = phi[cur] - phi[cur] / i;
cur += i;
}
}
}
return phi;
}
Thank You!!
You can always connect me: Aman Nadaf.
If you have any queries do not forget to leave a comment. You can always contact us below.