What is Convolutional Neural Network?
A Convolutional Neural Network (CNN) is a type of deep learning algorithm that is widely used for processing and analyzing visual data such as images and videos. CNNs consist of multiple layers of interconnected neurons, including convolutional layers, pooling layers, and fully connected layers.
Before CNNs, manual, time-consuming feature extraction methods were used to identify objects in images. However, convolutional neural networks now provide a more scalable approach to image classification and object recognition.
Key Terms
Before we get deep into CNN, let's understand few key terms first.
Neural Network: A computational model inspired by the structure and functionality of the human brain, consisting of interconnected nodes (neurons) that process and analyze information.
Convolution: The mathematical operation of applying a filter/kernel to the input data, which helps extract features by performing element wise multiplication and summation.
Convolutional Layer: The layer in a CNN that applies convolutional operations to the input data using one or more filters/kernels.
Filter/Kernel: A small matrix of weights that is convolved with the input data to produce a feature map.
Feature Map: The output of a convolutional layer, which represents the presence of specific features in the input data.
Pooling: A downsampling operation that reduces the spatial dimensions of the feature maps by selecting the most important or representative values.
Pooling Layer: The layer in a CNN that performs pooling operations to reduce the spatial dimensions and extract salient features from the feature maps.
Stride: The step size used to move the filter/kernel during the convolution operation.
Padding: Adding additional pixels or values around the input data to preserve spatial information during convolution.
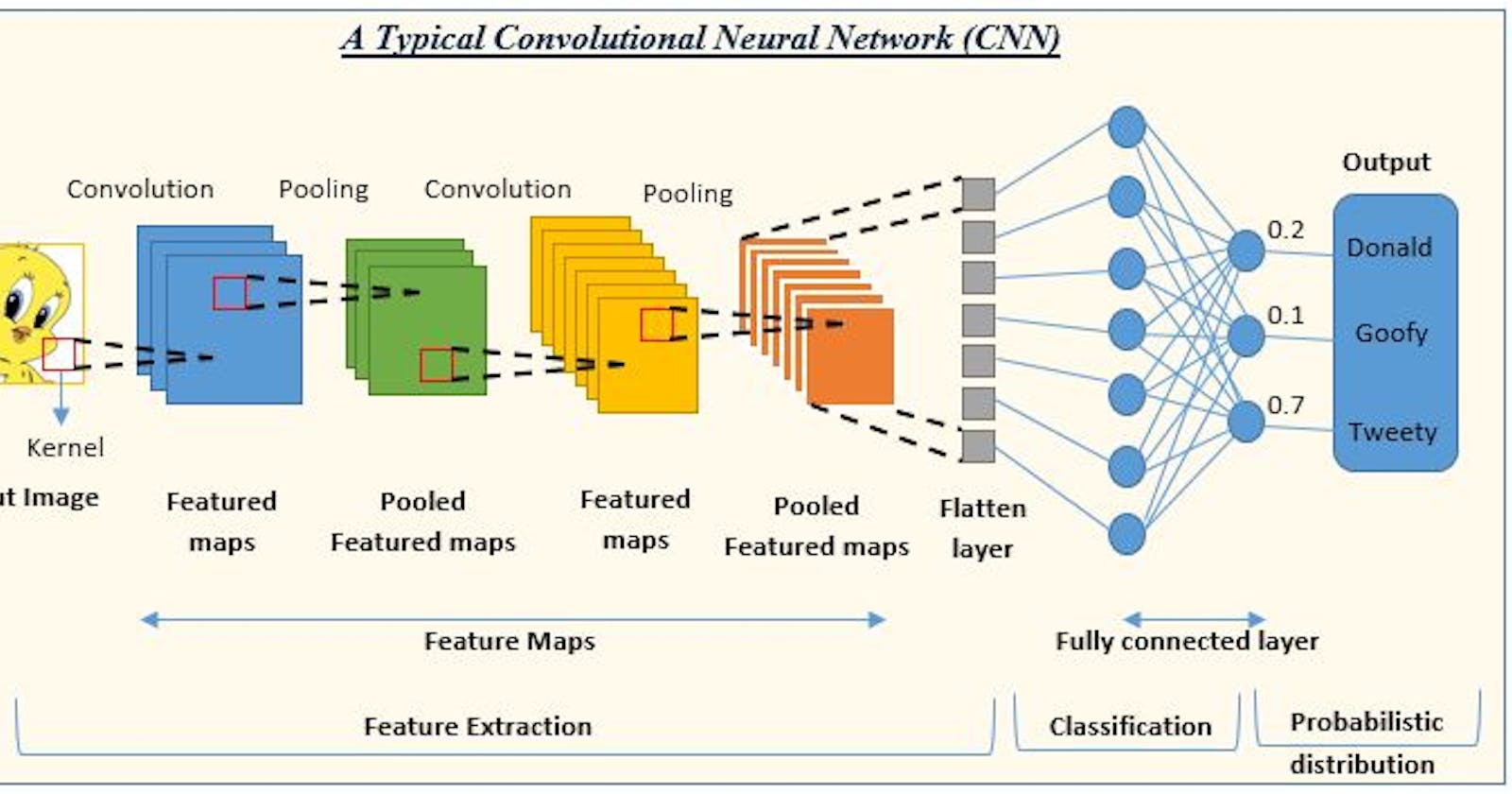
How CNN works?
Input Layer: The input to the CNN is typically an image or a set of images. Each image is represented as a grid of pixels, where each pixel contains color information (RGB values) or grayscale intensity.
Convolutional Layers: The CNN begins with one or more convolutional layers. Each convolutional layer consists of multiple filters/kernels, which are small matrices of weights. These filters are convolved with the input data using a sliding window approach. The filters detect specific features or patterns by performing element-wise multiplication and summation.
Activation Function: After the convolution operation, an activation function, such as ReLU (Rectified Linear Unit), is applied element-wise to introduce non-linearity.
Pooling Layers: To reduce the spatial dimensions of the feature maps and extract the most important information, pooling layers are added. Common types of pooling operations include max pooling or average pooling. Pooling helps reduce the number of parameters and computational complexity while retaining the most salient features.
Fully Connected Layers: After several convolutional and pooling layers, the feature maps are flattened into a one-dimensional vector. These flattened features are then passed to one or more fully connected layers, where each neuron is connected to every neuron in the previous and next layers. Fully connected layers are responsible for performing high-level feature representation and can be used for classification or regression tasks.
Output Layer: The final fully connected layer is typically followed by an output layer that produces the desired output. The number of neurons in the output layer depends on the specific task. For example, in image classification, the number of neurons in the output layer corresponds to the number of classes, and the output represents the probability distribution over the classes.
Loss Function and Optimization: During training, the CNN's output is compared to the true labels using a loss function, such as cross entropy. The loss function measures the discrepancy between the predicted output and the true output. The goal of the training process is to minimize this loss. Optimization algorithms, such as gradient descent, are used to iteratively adjust the weights of the network based on the computed gradients.
Backpropagation: Backpropagation is used to compute and propagate gradients through the network. The gradients are used to update the weights in a direction that reduces the loss. The process of forward propagation and backpropagation is repeated for a certain number of epochs to train the CNN. (Detailed Article coming soon)
Inference: Once the CNN is trained, it can be used for inference on new, unseen data. The input data is passed through the network, and the output is obtained from the output layer

Advantage of CNN
Hierarchical Feature Learning: CNNs are designed to automatically learn hierarchical representations of features. Convolutional layers capture low-level features like edges and textures, while deeper layers capture higher-level features like shapes and object parts. This hierarchical feature learning enables CNNs to extract meaningful representations from raw visual data.
Spatial Invariance: CNNs are able to achieve spatial invariance, meaning they can recognize patterns or features regardless of their location in the input data. This is achieved through the use of shared weights in convolutional layers, where the same filters are applied across the entire input, allowing the network to learn local patterns irrespective of their position.
Parameter Sharing: CNNs exploit the idea of parameter sharing, meaning that the same filters are applied to different spatial locations of the input. This significantly reduces the number of parameters in the network compared to fully connected networks, making CNNs more efficient in terms of memory usage and computational requirements.
Translation Invariance: CNNs are capable of achieving translation invariance, meaning they can recognize objects or features even if they are slightly shifted or translated in the input image. This is because the convolutional operation is performed at different locations across the input, allowing the network to capture local patterns irrespective of their precise location.
Sparse Connectivity: CNNs have sparse connectivity, which means that each neuron is only connected to a small local region of the input. This sparse connectivity reduces the computational complexity of the network and enables efficient processing of large-scale visual data.
Effective Parameter Learning: CNNs leverage gradient-based optimization techniques, such as backpropagation, to learn the optimal weights and parameters during training. This allows the network to adapt and improve its performance on specific tasks by minimizing the defined loss function.
Transfer Learning: CNNs trained on large datasets, such as ImageNet, can be used as feature extractors for new, smaller datasets. This transfer learning approach allows CNNs to leverage pre-trained knowledge and generalize well to new tasks even with limited training data.